
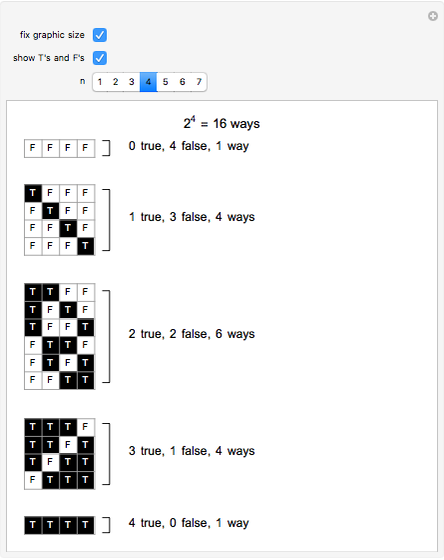
One thing this means is the notion that bugs in a program is not really relevant like it was (or like it is with other programming languages). You also have the simple programs like cellular automata.
TESTING WOLFRAM PLAYER CODE
Nowadays we think of all the different ways of interacting, from traditional code to dynamic graphical manipulations to natural language Wolfram Alpha queries, that all of these count as programming. It is worth noting that "what is a program" has evolved quite a bit. The latter could be the thing to test about Wolfram education. They examined Logo, the claims made about it, and concluded that it neither helped learn rigorous thinking (traditional math) nor was there evidence that it helped mathematical explorations (something the computer advocates were claiming). This one is about the cognitive effects of learning computer programming. I am not an expert and hardly familiar with educational research but found some old articles from the 1980s. The main one I think is the choice of programming language, and even the questions like what is a program and are there different ways of thinking. Maybe your questions highlight some paths for experimentation while exposing some possible problems.
You pose another interesting question which is "does programming in different languages affect the learning outcomes for students in different ways?". "does modeling a polymer improve one's understanding of polymer formation better than deriving the mathematical formulas?", as opposed to the bigger question of "does programming in general affect how one thinks?". My work is focused quite explicitly on looking at how learning to program within the context of a particular discipline affects learning, e.g. There are centers at places like Carnegie Mellon studying the topic in general. The terminology being used lately to describe the type of cognitive problem solving strategies learned through training in computer programming is "computational thinking". Side-stepping the naming of languages and returning to the original prompt, I am putting together a education platform to gather data and answer these types of research questions. The article by Sala and Gobet offers perhaps a bit of caution comes from its observation that the improvements might not be as great as other things, like learning music. But how could one measure it? It would seem wrong to measure something like the learning of formulas that the student no longer needs to learn. I've seen a high school dropout who did not know the line-slope formula (or any formula) pick up Wolfram Language and become very productive. I am not alone with anecdotal evidence that learning Wolfram language can make you smarter. One could just drop math altogether, but instead this is a way to still do math, just in a modern sort of way. More fun than memorizing facts and logical rules.
Among the range of alternatives to traditional education the possibility here is positive. Teach some useful skills with powerful software, possibly even in place of traditional mathematical education.


 0 kommentar(er)
0 kommentar(er)
